Analytic Function: in Real analysis you have studied about differentiable concept, but when we talk about complex analysis, the analytic function is same as differentiable Function. Just difference is space where the real one and here complex space.
Definition: Any function of a complex variable z is called analytic in open set if it has a derivative at each point in that set.
In other words
A complex valued function is said to be analytic at a point
if
exists and unique at .
Analytic Function is also called Regular function & Homomorphic Function.
To Find any Function is Analytic or not we use Cauchy Riemann (C-R) Equation. It is necessary condition but not sufficient condition.
Lets first discuss about the basic concept of ( z plane ).
Z-plane: It is just like a xy plane. it plays an important role in Mathematics. In Z plane Horizontal Line is called real line or Real Axis and vertical Line is called imaginary or complex Axis.
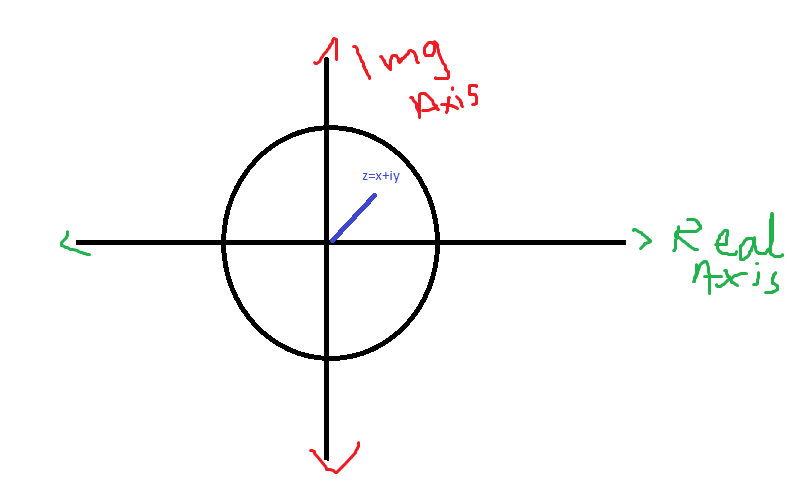
Any point in this plane is represented by here x represent real and iy represent imaginary axis.
Cauchy Riemann (C-R) Equation: A Function is analytic ( differential ) if it satisfies these equations.
For More Detail about This Topic Read this Book.
above book Name Functions of complex variables by sigma Network. Download in pdf form
Mathematics MCQs For PPSC FPSC NTS SS Download here
